Indefinite Integration of the Gamma Integral
and Related Statistical Applications
3.1 Explaining the "h" Function
In the previous section, the discussion of the "h" function was restricted to real numbers of the base parameter s, except negative integers. This restriction can be relaxed with the following definition of "h ":
\begin{equation*}
h_{s}^{c}=
\begin{cases}
\sum\limits_{i=0}^{\infty }{\frac{{{\left( -c \right)}^{i}}}{\prod\limits_{j=0}^{i}{\left( s+1+j \right)}}}
, &\text{if $s\notin {{\mathbb{Z}}^{-}}$;}\\
{\exp(-c)}\left( \log \left| c \right|+\sum\limits_{s=0}^{\infty }{h_{s}^{-c}} \right), &\text{if $s=-1$;}\\
\sum\limits_{i=0}^{-s-2}{\frac{{{\left( -c \right)}^{i}}}{\prod\limits_{j=0}^{i}{\left( s+1+j \right)}}+\frac{{{\left( -c
\right)}^{-s-1}}}{\prod\limits_{j=0}^{-s-2}{\left( s+1+j \right)}}}h_{-1}^{c}, &\text{if $s\in {{\mathbb{Z}}^{-}}$ & $s\ne -1$.}
\end{cases}
\tag{3.1}
\end{equation*}
[Definition of (3.1)]
When s is not a negative integer, "h" is regarded as the core function of the solution to the indefinite
gamma integral. Its asymptotic property at c\to -\infty directly links to the gamma function. When s is a negative integer, "h
" is related to the exponential integral, but only in the sense of definite integral. Specifically, we can apply h_{s}^{c} to an
nth-order exponential integral with a definite lower and upper limit a and b.
\begin{equation*}
\int_{a}^{b}{\frac{{\exp(-x)}}{{x}^{n}}}dx={{{x}^{-n+1}}}{\exp(-x)}h_{-n}^{-x}{\Bigr|}_{a}^{b}
\end{equation*}
The above formula is only meaningful if a and b are positive finite numbers. We can explain why that is the case by discussing the infinite series that defines h_{-1}^{c}. As (3.1) makes evident, h_{s}^{c} can be reduced to a function of h_{-1}^{c} when s belongs to negative integers. By definition, h_{-1}^{c} is a two-term product, in which the latter term is the sum of \log \left| c \right| and an infinite number h_{s}^{-c}, beginning at s=0 and extending to s\to \infty . Since all of h_{s}^{-c} are positive when s\ge 0, the value of h_{-1}^{c} is contingent on the actual number of terms, noted as "t" hereafter, used to compute \sum\limits_{s=0}^{\infty }{h_{s}^{-c}}. As a result, its numerical magnitude can not be interpreted directly as the antiderivative value in absolute terms.
When the upper limit is infinity, we encounter a problem in evaluating the asymptotic property of h_{-1}^{-c}{{|}_{c\to \infty }}. Fortunately, the finite property of the infinite upper limit applies to all of the "h" functions used in calculating h_{-1}^{-c}{{|}_{c\to \infty }}. Therefore, the error of replacing the infinite upper limit with a considerably larger number C is trivial.
We refer to two distinct sources of error in applying the "h" function to evaluate the exponential integral. The first is the actual number of terms t in the computation of h_{-1}^{c}. This is a pure numerical problem, and it is similar to the number of terms from a Taylor series we need to compute an exponential number. The second source of error comes from the evaluation of the "h" function when the power parameter c approaches infinity. A discussion of these two kinds of error can be found in Section 4.1 and 4.3.
The functional form of "h" does somewhat resembles exp, but "h" is not a Taylor series since the denominator is not a factorial term starting from 0!. If we set s=-1, all the denominator terms become 0 and "h" can not be defined by (2.1). Despite their difference, we can easily find certain identities between "h" and exp when s is a non-negative integer, such as h_{0}^{c}={\left[ 1-\exp (-c) \right]}/{c}.
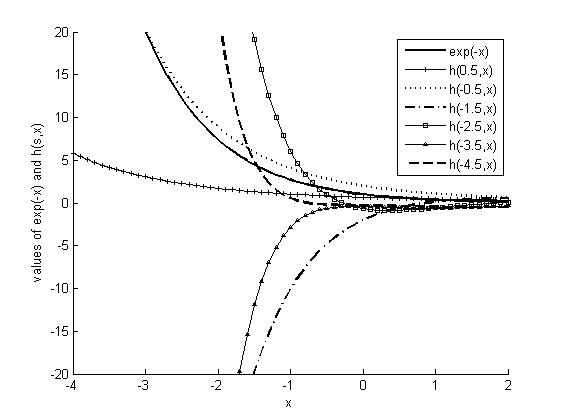
Figure 2: Functional Plots of {\exp(-x)} and h_{s}^{x}
Unlike the exponential function, the power parameter c of the "h" function takes a negative value in composing the series, and hence, the shape of y=h_{s}^{c} is downward-sloping and decreases to {{0}^{+}} as c increases to infinity, which is similar to the shape of the exponential function \exp \left( -x \right). In addition, the intercept value of the "h" function is {1}/{\left( s+1 \right)}, and this also differs from the case of the exponential function, which is always one.
Figure 2 presents functional plots of {\exp(-x)} and h_{s}^{x} with six different base parameters. Despite the similar shape, \exp \left( -x \right) intersects with all of the "h" functions. This clearly demonstrates that \exp \left( -x \right) and h_{s}^{x} are two distinct functions. When s>-1, h_{s}^{x} is a monotonically decreasing function from x=-\infty to x=\infty. When s<-1, the monotomic increase or decrease of h_{s}^{x} depends on the odd or even number of \left\lfloor s+1 \right\rfloor . If \left\lfloor s+1 \right\rfloor is an odd number, h_{s}^{x} is a monotonically increasing function, such as h_{-1.5}^{x} or h_{-3.5}^{x}; otherwise, h_{s}^{x} is a monotonically decreasing function, such as h_{-2.5}^{x} or h_{-4.5}^{x}
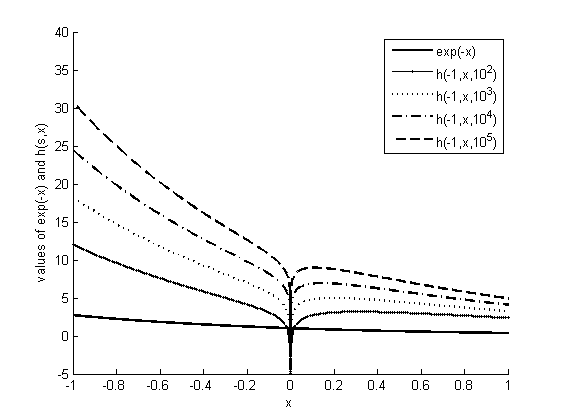
Figure 3: Functional Plots of {\exp(-x)} and h_{-1}^{x} by varying t
When s is a negative integer, an h_{s}^{x} function can be represented by an infinite number of curves. Each curve corresponds to a particular number of summation terms t that are used to compute \sum\limits_{s=0}^{\infty }{h_{s}^{-x}} for h_{-1}^{x} in (3.1). As explained in Section 4.3, each curve refers to the same h_{s}^{x} function but with different levels of computational accuracy. Figure 3 presents four indifferent curves of h_{s}^{x} with different levels of precision for one ({{10}^{2}}), two ({{10}^{3}}), three ({{10}^{4}}), and four ({{10}^{5}}) decimal places. Each set of parentheses contains the number of summation terms t for each curve.
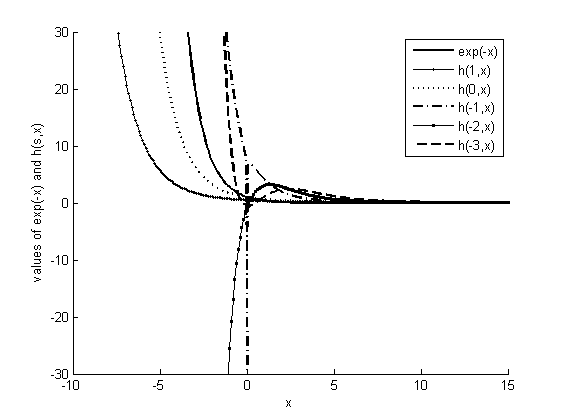
Figure 4: Functional Plots of {\exp(-x)} and h_{s}^{x} with three significant digits (if s\in {{\mathbb{Z}}^{-}})
Maintaining a constant precision level, we can also plot h_{s}^{x} when s is a negative integer. As Figure 4 shows, when the precision level is set to three decimal digits (t={10}^{4}), the "h" function monotonically decreases if s belongs to non-negative integers or odd negative integers, and it monotonically increases if s belongs to even negative integers. We should be aware that only h_{-1}^{x} has a singular point x=0, but the limit of the remaining "h" functions does exist and can be evaluated by {1}/{\left( s+1 \right)}.
Given that the functional value of "h" and the power parameter c have a one-to-one relationship, the inverse function of "h", denoted by {}^{-1}{{h}_{s}}\left( \delta \right), can be defined by the following infinite series and is very similar to a logarithmic function:
\begin{align*}
{}^{-1}{{h}_{s}}\left( \delta \right) =&-\left[ \left( s+1 \right)\left( s+2 \right)\delta-\left( s+2 \right) \right] \\ \notag
&+\frac{1}{\left( s+3 \right)}{{\left[ \left( s+1 \right)\left( s+2 \right)\delta-\left( s+2 \right) \right]}^{2}}\\ \notag
&-\frac{s+5}{{{\left( s+3 \right)}^{2}}\left( s+4 \right)}{{\left[ \left( s+1 \right)\left( s+2 \right)\delta-\left( s+2 \right)
\right]}^{3}} \\ \notag
&+\frac{{{s}^{2}}+11s+34}{{{\left( s+3 \right)}^{3}}\left( s+4 \right)\left( s+5 \right)}{{\left[ \left( s+1 \right)\left( s+2
\right)\delta-\left( s+2 \right) \right]}^{4}}+\cdots, \tag{3.2}
\end{align*}
where \delta=h_{s}^{c} and c={}^{-1}{{h}_{s}}\left( \delta \right).
[Proof for (3.2)]
To avoid confusing the inverse sign with the power parameter c=-1, we label the inverse function with a left superscript instead of a conventional right superscript. The formula c={}^{-1}{{h}_{s}}\left( \delta \right) in (3.2) can easily be derived from (2.1), and we display the first four terms here. Unfortunately, it usually requires many terms to approximate c, and it is more efficient to compute {}^{-1}{{h}_{s}} \left( \delta \right) with iterative methods by numerical analysis. For instance, if we know h_{1}^{c}=\delta, the relationship between c and \delta can be specified by (3.1) and reduced to the equation {{c}^{2}}\delta-c-{\exp(-c)}+1=0. Solving the equation through a numerical analysis will find the root of c, or the value of the inverse function {}^{-1}{{h}_{s}} \left( \delta \right).
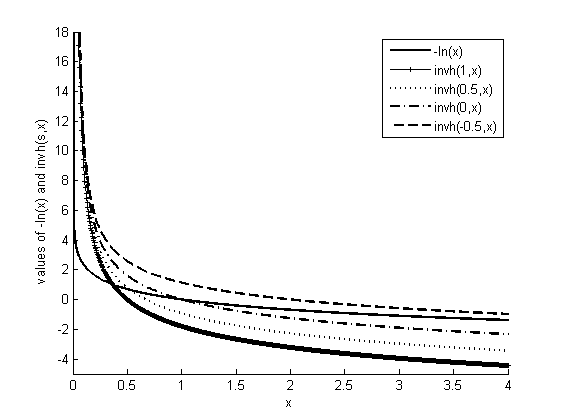
Figure 5: Functional Plots of -ln(x) and {}^{-1}{{h}_{s}}\left( x \right)
Figure 5 presents functional plots of -ln(x) and {}^{-1}{{h}_{s}}\left( x \right). Both functions have a similarly shaped curves, but -ln(x) intersects with all the curves of {}^{-1}{{h}_{s}}\left( x \right). Apparently, -ln(x) and {}^{-1}{{h}_{s}}\left( x \right) are distinct functions, too.
